Author: Jesper

Tuesday Changes Everything (a Mathematical Puzzle)

The last two weeks have seen heated debate about a mathematical puzzle posed by Gary Foshee and reported by  New Scientist (discussions here and here and here).

Gary Foshee, a collector and designer of puzzles from Issaquah near Seattle walked to the lectern to present his talk. It consisted of the following three sentences: “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”

“The first thing you think is ‘What has Tuesday got to do with it?'” said Foshee, deadpan. “Well, it has everything to do with it.” And then he stepped down from the stage.

This is the answer: 13/27.

Many people will intuitively say that the answer is 1/2 (=the chance of having a boy or a girl), but probability aficionados will give the answer 1/3, since this is the Boy or Girl Paradox: We are not told that the speaker has a child and is waiting for another, but that he already has two children. Two children can come in four configurations: 1) boy/girl, 2) girl/boy, 3) girl/girl, 4) boy/boy. Since he has one boy, we are looking at the options 1, 2, or 4. Only the boy/boy combination includes two boys, so the probability is 1/3. In other words, order matters and completely changes probability.

So what has being born on a Tuesday got to do with it? Why would the answer not still be 1/3? The New Scientist has a good explanation toward the bottom of the article. Simply count the different combinations of genders and weekdays, which gives the result (number of combinations with two boys, at least one of which was born on a Tuesday) / (number of combinations with at least one boy born on a Tuesday). The result really is 13/27.

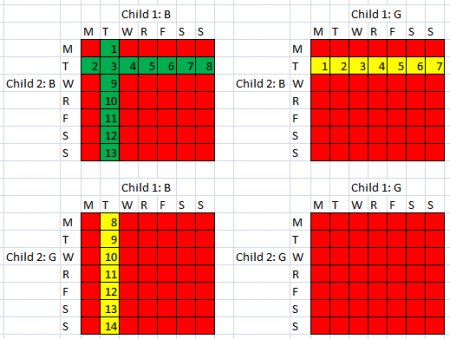
This is the best illustration I have found: This shows all the boy/girl pairs as well as the possible weekdays on which they could be born. Green represents situations with two boys, at least one of which was born on a Tuesday. Yellow represents at least one boy born on a Tuesday. Red is neither. Hence the answer is green/(green+yellow)= 13/(13+14)  = 13/27.

But again, what has Tuesday got to do with it?

More below.

Continue reading “Tuesday Changes Everything (a Mathematical Puzzle)”

Guimark2: Some HTML, Flash, Java benchmarks

And now for something completely different.

My past as a Commodore 64 demo programmer means that I find benchmarks quite irresistible. What is the fastest way to accomplish a given task?

Following Steve Jobs’ denunciation of Flash as slow, Sean Christmann recently posted his Guimark2 test suite for comparing vector, bitmap, and text rendering across platforms. Sean built Flash and HTML versions of the tests. One of the clear results was that HTML5 just isn’t that fast yet.

But being mostly a Java programmer, I couldn’t help building Java versions (perhaps I wanted to counter the perception that Java is slow). You can try the Java tests here, Vector, Bitmap, Text and compare them to the tests on the Guimark2 page.

Here are the results from the two machines I tested on:

Test/OS XP, HTML XP, Flash XP, Java OS X, HTML OS X, Flash OS X, Java
Vector 11.9 21.9 20.7 4.5 19.8 31.9
Bitmap 4.3 12.7 208.2 13.0 12.9 42.0
Text 19.2 1.5 11.4 29.9 16.6 14.1

Test results in Frames Per Second (Higher is better)

As you can see, on my two test machines, the Vector test is fastest in Java on OS X, the Bitmap test is fastest in Java on XP (5 times faster than any other platform/language), and the Text test is fastest in HTML on OS X.

Is this always the case? No. As can also be witnessed on the Guimark2 page, these results are highly variable between different OS configurations, browsers. As far as I can make out, really high Java bitmap scores require an ATI or NVidia graphics card, and may not always be present on Windows Vista or 7. On OS X, Flash runs faster in 32-bit Safari, while Java runs fastest in 64-bit Safari (tested here). And so on.

Benchmarking is a lot more complicated than it used to be, but I just thought I’d share these results. The tests also link to the source code if you are interested. Feel free to post your results here or on the Guimark2 page.

PS. Test machines:

  • 2007 Lenovo ThinkPad T60p running Windows XP, Firefox 3.6, Java 1.6, Flash 10.
  • 2010 15″ MacBook Pro running Snow Leopard, Safari (64-bit), Java 1.6, Flash 10.

More about Downsides to External Rewards

Following my earlier discussion of external rewards, here’s a video discussion how increased monetary rewards can lead to decreased performance. The studies mentioned here suggest that monetary rewards work well for mechanical tasks, but have negative impact on cognitively challenging tasks.

The video then discusses how things like open source and personal purpose fly in the face of traditional ideas of economical incentives.

There are many things to say about this, but I have been entertaining the idea that the “surprising finds” in the video are an artifact of a cognitive bias: Many people (such as economists) are fully aware that they are personally motivated by many different things such as pride, ambition, personal interests, social relations and so on … but nevertheless assume that everybody else is only motivated by money and gold stars.

Silly, isn’t it?

*

I am not sure how directly this can be translated into the question of achievements and rewards in video games as there appear to be big differences between monetary and symbolic rewards. More about that later.

Bejeweled: Game of the Decade

Over at Htlit.com, I have a short text arguing that Bejeweled is the most important game of the 2000’s (the decade, that is). (Waiting for the protests from a crowd of angry gamers.)

Viewed strictly as a game design, this probably isn’t the most enjoyable game of the decade. Neither is it the most innovative, being rather an incremental development based of a number of existing designs.What makes Bejeweled the game of the decade is its central role in the casual revolution: This game was instrumental in creating the first video game distribution channel aimed at an older and predominantly female audience (downloadable casual games), hence redefining our ideas of what a video game could be and who could play video games. Furthermore, its basic gameplay of swapping tiles to make colored matches has taken on a life of its own, now playable on cell phones and aeroplanes; as relaxed game sessions without any time pressure; packaged as a role-playing game set in a fantasy world (Puzzle Quest); as a one-minute intensive game for competing against friends (Bejeweled Blitz). That is the importance of Bejeweled: showing us how many different things video games can be, showing us that there are many ways to play, use, and enjoy video games.

Pac-Man 30 years; playable on Google.com

Pac-Man is officially 30 years old today. (This is what the internet has settled on, even though Bandai claims that it’s tomorrow.)

Just this morning the cleaning lady here professed that Pac-Man was her favorite of the arcade games we have in the NYU Game Center.

And I do think it is one of the few arcade games that remains as playable today as it was 20 or 30 years ago. Is it the Citizen Kane of video games? How would we tell? What would that mean? It certainly has a kind of internal coherence and perfection, a stylized graphical style that does not date, a gameplay that is clear, strategies that are sufficiently interesting, and little tricks like the fact that the ghosts switch between aiming for the player and wandering aimlessly, leading to many exciting near misses. It works.

It also happens to be playable on google.com:

Update: News.com writeup on Pac-Man, Google’s implementation.

Recent Theses: Abstract Games, Character-Driven Game Design, the Mind Module

Here are three interesting recent video game Master and PhD theses for your theoretical enjoyment.

*

Jason Begy’s (my former research assistant at GAMBIT) Comparative Media Studies thesis:

Interpreting Abstract Games: The Metaphorical Potential of Formal Game Elements

*

Petri Lankoski’s PhD thesis, Aalto University:

*

Mirjam Palosaari Eladhari’s PhD thesis, Teeside University:

Characterising Action Potential in Virtual Game Worlds Applied with the Mind Module

Game Studies 10/01 is Out

(Yes, 10 years of Game Studies!)
*

by J. Alison Bryant, Anna Akerman, Jordana Drell

This article details the “user-centered” research process adopted to create Nintendo DS games for preschoolers and addresses how new titles for specific populations can be approached. We review the role of exploratory and formative research in game development for young audiences and provide findings and design tips from the laboratory and field. [more]
*
Tags, Threads, and Frames: Toward a Synthesis of Interaction Ritual and Livejournal Roleplaying
by Sarah Wanenchak

This paper examines a game where sociological rules of interaction are adapted to fit an online context free from face to face encounters, and where these adapted rules are further stretched to fit interactions designed to construct a narrative that exists on both the individual and the communal levels. [more]
*

Game designers often limit the availability of powerful cards in collectible card games. This approach can have negative consequences on a game’s suitability for casual play. This paper explores case studies of two online collectible card games and a design philosophy that argues that powerful game effects should be commonly available to players. [more]

*
This article criticises influential MMO scholarship approaching virtual worlds as if they were outside the real world, and presents an alternative view based on Anselm Strauss’s concept of overlapping social worlds. MMOs are seen as sites where the world of players meshes with families and workplaces, and often flows over to other sites and forums. [more]

Interview

by Celia Pearce
Rand Miller, who with his brother Robyn designed Myst, the first blockbuster CD-ROM, talks about his legacy of vanguard game design, and the complex history of its multiplayer sequel Uru: Ages Beyond Myst. This interview, conducted via e-mail, took place shortly before the third re-opening of Uru. [more]

Book Reviews

by Richard Bartle
Review of “Digital Culture, Play and Identity: A World of Warcraft Reader” edited by Hilde G. Corneliussen and Jill Walker Rettberg, (MIT Press, 2008). [more]
*
by Frans Mäyrä Review of “Cheating: Gaining Advantage in Videogames” by Mia Consalvo, (MIT Press 2007). [more]
*
by Cynthia Haynes
Review of “Critical Play: Radical Game Design” by Mary Flanagan (MIT Press, 2009) [more]
*
by Ragnhild Tronstad
Review of “Critical Play: Radical Game Design” by Mary Flanagan, (MIT Press, 2009). [more]