The last two weeks have seen heated debate about a mathematical puzzle posed by Gary Foshee and reported by New Scientist (discussions here and here and here).
Gary Foshee, a collector and designer of puzzles from Issaquah near Seattle walked to the lectern to present his talk. It consisted of the following three sentences: “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”
“The first thing you think is ‘What has Tuesday got to do with it?'” said Foshee, deadpan. “Well, it has everything to do with it.” And then he stepped down from the stage.
This is the answer: 13/27.
Many people will intuitively say that the answer is 1/2 (=the chance of having a boy or a girl), but probability aficionados will give the answer 1/3, since this is the Boy or Girl Paradox: We are not told that the speaker has a child and is waiting for another, but that he already has two children. Two children can come in four configurations: 1) boy/girl, 2) girl/boy, 3) girl/girl, 4) boy/boy. Since he has one boy, we are looking at the options 1, 2, or 4. Only the boy/boy combination includes two boys, so the probability is 1/3. In other words, order matters and completely changes probability.
So what has being born on a Tuesday got to do with it? Why would the answer not still be 1/3? The New Scientist has a good explanation toward the bottom of the article. Simply count the different combinations of genders and weekdays, which gives the result (number of combinations with two boys, at least one of which was born on a Tuesday) / (number of combinations with at least one boy born on a Tuesday). The result really is 13/27.
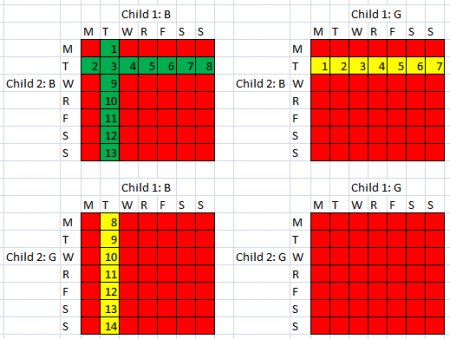
This is the best illustration I have found: This shows all the boy/girl pairs as well as the possible weekdays on which they could be born. Green represents situations with two boys, at least one of which was born on a Tuesday. Yellow represents at least one boy born on a Tuesday. Red is neither. Hence the answer is green/(green+yellow)= 13/(13+14) = 13/27.
But again, what has Tuesday got to do with it?
More below.
Discussion
It is an appealing puzzle because even once you (or at least I) accept the 13/27 calculation and visualize it, it still is wildly counter-intuitive that being born on a Tuesday influences the probability of having a brother. (Actually it doesn’t – see below.) What’s also strange is that with a rarer trait (say, being born on February 29), the probability of having two boys approaches 1/2. (For a trait with probability 1/A, the probability of having two boys is 2A-1/4A-1.)
Other people with more skill in probability theory have explained it well (search for “cocktail party” here), but I thought about it moving backwards from the result: Our intuition (which is correct) is that boys born on Tuesdays do not have a larger chance of having a brother than boys born on other days. Therefore the 13/27 result seems absurd because we could repeat it with all days of the week, add up the results, and reach the conclusion that the answer to the boy or girl paradox was 13/27 and not 1/3. And that is the hint: We are not really calculating what we think we are calculating.
It is really a question of formulation. The puzzle is not “My firstborn is a boy born on Tuesday” or “I have exactly one boy born on a Tuesday”, but “One [or more] is a boy born on a Tuesday [but I am not telling you which one].” Which means that we did not calculate whether being born on a Tuesday influences the probability of having a brother.
As I stated above, the absurdity comes from the fact that we might imagine that we had sliced the possibility space (2 genders, 7 weekdays) into 7 equally big slices, but did we? Try repeating the calculation for “boy born on a Tuesday”, “boy born on a Wednesday” etc…
Now consider the case of the oldest child being a boy born on a Tuesday, and the youngest child being a boy born on a Wednesday. This will count toward both the probability of “two boys when at least one child is a boy born on a Tuesday” and “two boys when at least one child is a boy born on a Wednesday”. Many cases are counted for several weekdays. This is why the probability goes up from the expected 1/3, approaching 1/2.
Why this is such a good puzzle:
- It is a puzzle within a puzzle.
- Like the Boy or Girl Paradox, which encourages us to answer from the knowledge that the boy/girl probability is (roughly) 50%, this puzzle encourages us to answer from the knowledge that being born on a given weekday generally doesn’t influence other probabilities. In both cases, that is not what the puzzle is actually asking us. We are tricked into using a stock answer that is not appropriate for the given puzzle.
- It appeals to puzzle and probability theory fans by building on an existing puzzle.
- It gives a result (approaching 1/2) which is exactly the result that connoisseurs know should not be the answer.
- It uses a counting technique specifically designed to prevent from counting the same case twice, and we may be thinking that “at least I am not counting anything twice”, but that is exactly what we are doing.
- The very terse explanation of the puzzle is deliberately misleading. When Foshee says ‘One is a boy born on a Tuesday. … What has Tuesday got to do with it? Well, it has everything to do with it.“, it makes it sound like we are doing a probability calculation depending on one particular boy, when in fact we are doing a calculation depending on “one or more children being a boy born on a Tuesday” – hence we end up counting some combinations for several weekdays.

If you like this, you should also check out ‘the monty hall problem’
Ah yes, that problem is similar in that we think we “know better” than to believe that opening one door changes the probabilities of the other doors, but that is exactly what happens.
Why on earth should order matter? I have problems agreeing with this:
“Two children can come in four configurations: 1) boy/girl, 2) girl/boy, 3) girl/girl, 4) boy/boy. Since he has one boy, we are looking at the options 1, 2, or 4. Only the boy/boy combination includes two boys, so the probability is 1/3. In other words, order matters and completely changes probability.”
The question was “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”
There’s two kids. You can have THREE combinations of two kids if all you’re looking at is which ones you have, not in which order you got them (which is not part of this question at all). B/B, G/G, B/G. We know it is not G/G. That leaves two possibilities, either B/B or B/G. The chance thus is 0.5.
Looking at the comments on those other posts about the puzzle seems to confirm I’m not alone in believing this, various apparently knowledgable people questioned the importance of order in this case. Even with math only being a small part of my university education I just can’t agree with order being of importance here. Seems like a typical case of specialists not seeing the forest for the trees.
see this reply at the original post:
“I think the problem is the vagueness of the problem statement. 13/27 is the answer to the question, “What is the probability that I have two boys, at least one of whom was born on Tuesday?” And 1/2 is the answer to the question, “Given this boy born on Tuesday wearing green socks, what is the probability of this other child being a boy?””
That’s exactly the problem. The question as originally asked leads to 0.5. There’s no reason whatsoever to interpret the original question in the first way.
So I seem to have confused myself. Perhaps you’ll be able to help.
I’ll start with the following premises.
(1) The answer to the question “A woman has two children, what is the probability that they are the same gender.” is 1/2.
(2) All children possess both a gender and a day of the week they were born on.
(3) The question posed in the post above has the same answer no matter what gender or day of the week you pick – 13/27.
Imagine I’m conducting a telephone survey of mothers with two-children. I ring them up and they say the following sentence:
“I have two children. One of them is a -gender- who was born on a -day of the week-.” To fill in the gaps they pick one of their two children at random.
I ring one particular woman but there’s a bad line. All I hear is:
“I have two children. One of them is a -brzt- who was born on -brzt-.” Then it cuts out. What is the probability that both of her children are the same gender?
It seems like it ought to be 1/2 because we don’t know ANYTHING about her children and so it’s just the question posed in (1). Yet by (2) and (3) it ought to be 12/37, since however you fill the gaps you get a question with that answer.
I can’t help but feel I’m being a bit dense.
Jan
Some of what you have said is true: “You can have THREE combinations of two kids if all you’re looking at is which ones you have, not in which order you got them (which is not part of this question at all). B/B, G/G, B/G. We know it is not G/G. That leaves two possibilities, either B/B or B/G.”
However, the last bit, “The chance thus is 0.5.” would only be true if the chance of B/B was the same as the chance of B/G. Unfortunately that is not the case: for every 100 B/B families, there are 100 G/G families and 200 B/G families. If you don’t believe that, it is easy to check by spinning coins. Spin two coins and note how many times you get head/head, how many tail/tail and how many head/tail. After a reasonable number of goes you will see that you are getting head/tail about twice as often as you get head/head or tail/tail.
That means that in your statement “That leaves two possibilities, either B/B or B/G” the weight of B/B is 1, but the weight of B/G is 2, so the case B/B is 1 out of 3, not one out of 2. To simulate it in the coin tossing, cross out the head/head count, and see what fraction of the remaining total (or tail/tail and head/tail) are tail/tail – it should be 1/3.
I hope that helps. I still find the “Tuesday” bit very hard to get my head round, although I’m willing to trust the maths rather than my “common sense.”
@Jan First of all, I spent a lot of time being frustrated with these answers myself, but I have come to believe that they are correct.
Concerning the first issue, whether the probability of having two boys is 1/3 or 1/2 if there are two children, at least one of whom is a boy:
I assume we agree that every child born has a 50% chance of being a girl or a boy.
The probabilities for first child are therefore:
Boy: 50%
Girl 50%.
If we repeat this for the second child, we get the probabilities:
Boy/Boy: 25%
Boy/Girl: 25%
Girl/Boy: 25%
Girl/Girl: 25%
That is why you cannot disregard the order of the children, The Boy/Girl and Girl/Boy combinations represent 50% of the total probability. Therefore the answer is 1/3.
As for the second problem with Tuesdays, I completely agree that it hinges on what exactly the question is. I do think though that “What is the probability that I have two boys, at least one of whom was born on Tuesday?” … is even less precise than the original since it doesn’t state how many children the speaker has in the first place.
But certainly the whole thing is a puzzle due to the way the question is phrased.
I agree with you though that once you start talking about “this” child, then the probability of having two boys jumps to 1/2. Note how the original question deliberately avoids talking about “this” boy.
@Nigel and Jesper
Yeah, just came back to post that I realised my error about 1/2 vs. 1/3. It is still 0.5 though. Why? Because we are making an error if we look at the 2-tupels B/G etc.. Yes, the question is about the pair of children. But, we’re still looking at only one child here. We know one is a boy so the question “what’s the chance that I have two boys” (and the question is only that, everything else is hidden and was not part of the actual question/puzzle) is the same as “what’s the chance to get a boy if I already have one”. Now it becomes obvious the existence of the first son is completely irrelevant and it all boils down to what’s the chance of getting a son, which is (theoretically) 0.5.
About the “puzzle”. This puzzle is not fair and should not be asked that way. It’s like asking what’s the chance of rolling a 6 with a dice and telling you afterwards that the dice had 7 sides.
@Rich The best explanation I have found is if you follow this link and search for “cocktail party”.
Basically the 13/27 result comes about because many child combinations are counted several times. It comes down to how the counting is done. Quoting from the cocktail party explanation:
It’s funny—I really like this puzzle, and think it’s generally a good demonstration of the perils of Bayesian logic and the value of perhaps sidestepping it in favor of a “spatially represented possible worlds” method, as nicely shown in those grids. This is an incredibly important skill, I think—as illustrated by this Stephen Strogatz article—as well as a surprisingly difficult one to develop—as illustrated by this Keith Devlin book, which makes it clear just how mind-bendingly difficult it was for top-drawer mathematicians like Pascal and Fermat to wrap their heads around how probability really works.
But I call shenanigans on the “terse, deliberately misleading” explanation, which is not a reason that this is a good, satisfying puzzle, but in fact the flaw that prevents it from being one. It’s not like the puzzle wouldn’t still be interesting and counterintuitively difficult if it was made clear that “One” was being used to mean “At least one” instead of the more natural-language meaning of “Exactly one,” and as semantic tricks go, this strikes me as about the same level of cheapness as saying “The sky is blue” and then making fun of someone for assuming you meant it wasn’t mottled by giant hot-pink polka dots. It’s also worth noting that on the only American logic puzzles of general real-world consequence—the LSAT, which largely determines what tier of law school applicants get into—the puzzle-makers always make sure to make it clear whether they mean “At least” or “Exactly” without requiring you to telepathically suss the author’s intent, as this puzzle does. Probably because otherwise, they would have gotten sued by some grudge-holding safety-law-school grad a long time ago, and rightly so—it’s a cheap trick, and one unworthy of a Martin Gardner fan.
Can I be the pedant here and point out there is one key problem with the given information? http://en.wikipedia.org/wiki/Sex_ratio
This is indeed an interesting puzzle, and its consequences are one reason I like to reference Inevitable Illusions (Piattelli-Palmarini) so often.
This is also the sort of counter-intuitive consequence that, while appealing within *games*, is not so appealing (and, in fact, actively avoided) in *virtual worlds*. Within the virtual world (built to appease rather than befuddle), it’s likely that code would be written so that the intuitive response to this puzzle (say 1/2 or 1/3) would become the actual (virtual) outcome. Or, more broadly: the psychophysical (what we feel the world should be) would replace the physical (what the world is).
I’m moved to post because there is currently a nice analysis of this very circumstance at the Greedy Goblin that talks about the “normalization of deviance” and the consequences thereof: what appears to be a game (Wintergrasp) is, in fact, not a game at all (or at least not a very good one). But, within a virtual world ruled by the socials (as Gevlon would call them), who will ever know?
@Jesse F, dmyers
The meta question then is whether the puzzle was playing within the rules or not. Certainly, when presented (as it was) at a meeting about puzzles, the audience will expect to have to watch out for little things like the possibility that “one” could mean “one or more”.
@Jesper That’s an excellent point; I didn’t really think about the original context, since I encountered in the context of being sent it by email and just trying to solve the thing as a civilian. But yeah, the original context is maybe the only place where not only would that sort of semantic trick be a _totally_ clean shot, but where attendees would probably feel offended and condescended to if the puzzle spelled it out as the LSAT would. Well, other than a bottle djinn/Faustian demon convention, where they probably have whole panel discussions on this sort of thing.
So I guess this is just a good example of how the fairness of a set of rules can be changed by a change in context and a subsequent collision of community expectations—something I’m pretty sure dmyers is talking about by referencing that WoW-related bone of contention, and which for me is exemplified by the near-inevitable abortive stalemate of mutual disgust that is the result of any game of Scrabble between a tournament player and a civilian.
Forshees calculation is fantastic because it has convinced a whole lot of people that their intutions is completely fooled. But the problem is – the calculations is wrong, but the error is well hidden.
This will explain where the flaw is, and the keys is: Not all outcomes is nessesarily equally weigted:
After the “two children, at least one boy” information we have 3 combinations of the children: BG, GB and BB, as we all probably know. Then let’s merge the weekday information into each specific child combination:
1 – Boy-Girl:
Foshee have told us, that one of the children is a boy, and he’s born on a Tuesday.
In this case it’s 100% certain that his is speaking of the first child, even if the audiences don’t know it (This is actually an important note, as you will see later).
The boy with the specified weekday is called BX (X because it’s irrelevant what weekday the boy is born). So we get these 7 possible combinations: BX-GMon, BX-GTue, BX-GWed, BX-GThu, BX-GFri, BX-GSat and BX-GSun.
2 – Girl-Boy:
Same story: 7 possible combinations: GMon-BX, GTue-BX….
3 – Boy Boy
Now it’s getting interesting. Foshee now have to choose which boy he will reveal the weekday of birth.
BUT – he can only choose one of them! Let’s say Foshee has no preference, so each boy have ONLY 50% CHANCE to be picked.
Each boy delivers 7 combinations (BX-BMon…. and Bmon-Bx…) which gives 14 combinations, but because the chance of each boy to be chosen is only 50%, then the weight of each combination have to be DIVIDED BY 2!
And so the final odds of a 2-boy situation will add up to 1/3 – just as your intuition tells you. ;-)
@Peder
I think you are making a mistake saying that Foshee has to choose. Try imagining a room full of fathers, each of which has one of the possible combination of genders and weekdays. That’s 2 genders (first child) * 7 weekdays (first child) * 2 genders (second child) * 7 weekdays (second child), so there are 196 fathers in the room to cover every possibility.
As described in the “cocktail party” explanation above, the puzzle is usually interpreted to mean “the chance of having two boys, having two children, with at least one being a boy born on a Tuesday”.
To answer that, we ask everybody to leave the room except the fathers who have at least one boy born on a Tuesday.
This leaves: 7 (from the boy-girl group) + 7 (from the girl-boy group) and 13 (from the boy-boy group), so we have 27 people in the room.
Then we ask everybody to leave who doesn’t have two boys. 7+7 (boy-girl and girl-boy) leave. So we have 13 people in the room.
This is why the result is 13/27.
****
You are answering a different puzzle because you are asking the father to choose which boy they are referring to: In that case, we have our 196 fathers in the room. We ask everybody who doesn’t have a boy to leave. (7*7=49 fathers leave) Then we ask every father to randomly tell us the weekday on which one of their boys were born. Everybody who didn’t say “Tuesday” is asked to leave.
This leaves: 7 (from the boy-girl group) + 7 (from the girl-boy group) and 7 (on average, from the boy-boy group), so we have 21 people in the room.
Then we ask everybody to leave who doesn’t have two boys. 7+7 (boy-girl and girl-boy) leave. So we have 7 people in the room.
In this case the result is 7/21 = 1/3 as you say.
So I think you are on to something, but I don’t believe you are answering the puzzle as it is stated.
The answer is a third, as Poul correctly says. The following story illustrates the nonsense of 13/27:-
“Following a terrible civil war in a third world country, there were 147 orphaned two-child families who were the subject of a mass adoption scheme. It happened that these 147 families all had at least one boy in them and that the group of 147 exactly met the even statistical distribution of BB BG and GB and days of birth that we have been discussing.There were 294 children of which 196 were boys and 98 girls.
147 sets of potential parents were assembled and told that there was to be a ballot whereby one family would be allocated to each set of parents in turn. It was explained that the probability of being allocated a two-boy family was 1/3 and a family comprising a boy and a girl 2/3.
Now it so happened that one of the parents was a clever statistician who knew that if he could get hold of a family where the boy’s day of birth was known then the probability of a two-boy family would rise to 13/27.
He made the mistake though of telling his friend this information and soon this fact was known throughout the whole gathering. As a result the parents, who all preferred boys to girls, insisted on asking for a family where the boy’s day of birth was known.
So the families were allocated to the parents in turn just after the organisers had announced the day of each boy’s birth.
So in this way 13/27 of the parents ended up with two boys, and 14/27 ended up with one girl and one boy. So the number of boys had increased from 194 to 217.78, and the number of girls had decreased from 98 to 76.23
The statistician was thanked deeply by the rest of the parents for bringing about this miracle.”
@ron
The mistake in the story you tell is in “the”: “the boy’s day of birth”.
The 13/27 calculation comes from the setup I explained above (selecting the subgroup of fathers who have a boy born on a Tuesday, rather than asking them to tell us which specific weekday a given boy was born on).
The 13/27 calculation does not increase the number of boys as your story would suggest, it simply means that many pairs of boys will be counted on several weekdays.
As the story points out, there are 147 families with at least one boy – if you divide that into weekdays, you get 21 families per weekday. There will be 7 families with two boys the first of which is born on that given weekday. The probability is 7/21 = 1/3.
The 13/27 then comes from the fact that if you ask whether the families have a boy born on a given weekday, you include another 6 families per weekday (boy on Tuesday + boy on all other weekdays are counted for both Tuesday and for the other weekday).
This adds 6 to both parts of the fraction: (7+6)/(21+6) = 13/27.
So, no, knowing the weekday on which a child is born does not by itself change probabilities, but asking the question is such a way that boy+boy pairs are counted several times does. The answer really is 13/27.
Jesper,
We both know that Foshee phrased the question so that it gave a counter-intuitive answer (13/27). The answer is correct at a superficial level, but it has no statistical integrity. Foshee and others have implied that the answer changes the probability of two boys in the given circumstances merely by adding the birth day of the boy mentioned, which, of course it does not. My story merely repeated this nonsense to prove that the idea is silly. I think we are agreed on this.
Where we disagree is that the answer “really is” 13/27.
The reason 13/27 has no integrity is that the statement given (i.e that the boy mentioned was born on a Tuesday) is a statement about a SINGLE birth. You cannot apply such a statement to a family of two and have it make sense. The wording is too imprecise.
I could argue that the probability space of the 42 Boy Boy families where the birth days of the two boys are different should be divided into two (unlike the 7 Boy Boy families where there are two boys born on the same day, and all of the Boy Girl families where the birth day of the boy is indisputable). This would give the correct and intuitive answer to THE THRUST of their argument about the probability of a two child family with at least one boy – which is 1/3.
But we are really both saying the same thing from a numbers point of view.
@ron
Well, it’s a puzzle, so the name of the game is to force us to rethink our intuitive way of solving the problem. I don’t think there is anything wrong with the problem statement – it tricks us into thinking about the problem in the wrong way, but that is what makes it a good puzzle.
I think the story you quoted is completely misleading because it gives the erroneous impression that the puzzle produces more boys. It does not.
That is what the whole puzzle is about in a sense – the puzzle is counter-intuitive because it sounds like selecting the Tuesday increases the chance of having a second boy, but what the puzzle actually does is change the selection of children on which the probability is calculated.
In short: I think it’s infuriating because it is a good puzzle, but the answer to the question “what is the chance of having two boys, having two children, with at least one being a boy born on a Tuesday” really is 13/27.
Jesper,
The problem with the 13/27 solution for some of us is this:
Each of the 27 families within the 147 family set in question has a notional probability of 1/147 within that set, if the 13/27 solution is correct. Now, since the 13/27 fraction applies equally to the other 6 days of the week as well as Tuesday, we appear to have 7 X 27 = 189 equally probable spaces of 1/147 within the set. (Based on the obvious fact that a child must be born on one day and that those probabilities need to add up to 1.)
The problem for us “deniers” is that we have had to resort to long-winded explanations or stories like mine , above, to illustrate our point. Now though comes an elegant argument from Sam, on Alex Bellos’s website.
http://alexbellos.com/?p=725#comments
Not sure whether the url link works but here is what Sam says:-
“This may appear repetitive but please read with full critical thinking turned on and bias turned off:
Ann has 2 children sitting on separate chairs behind a screen. She tells you that she has a boy. What is the probability that the other child is also a boy?
Note that Ann’s statement is TRUE. She is saying that of her 2 children, 1 is a boy and for whatever reason she is referring to that particular child. She has told you nothing about the other child, but you know the probability of boy or girl is equal (for our purposes).
We can logically lay out the cases, making sure to keep the instances of children either sitting on the left chair or the right chair:
Ann’s children probability space given her statement:
L R
===
B B
B G
G B
There are only 3 possible arrangements for her children and we see by inspection there is 1/3 probability that there is a second boy behind the screen, the single BB case.
Note that in the BB case, Ann was referring to one and only one of the possible boy children, the one on the left, say. We don’t know which, but we do know that whichever one she was referring to she was NOT referring to the other one. This is fundamental to understanding the problem.
Then Bob comes in and tells us he too has 2 children behind a screen sitting on chairs, and 1 is a boy born on a Tuesday. Bob’s statement is TRUE.
Bob’s children probability space given his statement:
L R
===
B B
B G
G B
Again he is referring to one and only one of his children. He knows what the arrangement is behind the screen, so in either of the 3 mutually exclusive cases above he is referring to either:
1.The boy on the left chair OR the boy on the right chair
2.The boy who happens to be on the left chair.
3.The boy who happens to be on the right chair.
Remember, Bob has complete knowledge about his children. He told you about one of them. The one he IS referring to WAS born on a Tuesday.
But for us trying to assess what is behind the screen all we know is that he is only referring to 1 child. In the BB case, we cannot distinguish which one is the one he is referring to, but we know he refers to only one of them.
The probability of the other one being a boy is therefore unchanged from the Ann scenario when we add some spurious additional information about the child he is already referring to.
You can prove there are only 3 distinct cases by asking Bob to write down which chair the boy he is referring to is sitting, left or right.”
Food fror thought, Jesper?
@ron
The reason that you are not getting 13/27 is that you are interpreting the problem statement in a different way than I am (or Foshee is).
A) If one, as you do, interprets it to mean that the speaker first selects one particular boy, and then adds some additional information, then you are correct, the answer is 1/3.
(In my example above, this corresponds to the fathers having to select a boy, then say the weekday aloud, and then have all the fathers that did not say Tuesday leave the room.)
B) Foshee (and the rest of the 13/27 camp) interprets it mean that gender and weekday selection is simultaneous. In my example above, you ask every father without a boy born on a Tuesday to leave the room. In this interpretation of the question, the result really is 13/27.
The different results simply come from different interpretations of the problem statement. It has nothing to do with the math, it’s just because you are interpreting the problem statement differently – which of course is what the puzzle is trying to trick you into doing.
I think the only way to really deny the 13/27 result is to say that you think that there is no way the problem statement can be interpreted in the way Foshee is suggesting.
Jesper
you’re clarity and understanding of the problem (and the meta problem) is among the very best I’ve seen. I agree with everything you say except the interpretation of Foshee’s initial question.
In deriving a set of all families with 2 children that have a boy with a certain characteristic, of course you are going to select more 2-boy families than naturally occur.
There is NOTHING in Foshee’s statement to say that any such screening has occurred and that Foshee’s family is anything other than a normally (binomially?) distributed family. Hence 1/3 is the only possible answer for the question as posed.
Thoughts?
Sam
The reason these kind of puzzles are so counter-intuitive is not (IMHO) that Bayesian probabity theory is counter-intuitive, but that the situations are extremely contrived. Take the simpler puzzle, “I have two children, one of them is a boy. What is the probability that the other child is a boy?”. To get the “correct” answer 1/3, you must either assume that the punster would never say “I have two children, one of them is a girl” unless he had two girls, or that he would not have posed the riddle at all if he had two girls.
Let’s try and analyze an alternative to this, e.g. that the punster is equally likely to mention the sex of any of his two children. Using Bayes theorem,
p(a|b)=p(b|a)*p(a)/p(b)
(“a” being that he has two boys, “b” is that he mentions a boy), we have the probability that he has two boys when he mentions a boy equal to the probability that he mentions a boy when he has two boys (1/1) times the probability that he as two boys (1/4) divided by the probability that he mentions a boy (1/2). The result is 1/2, or 50%, which is what most people would guess at first try.
Similarly, we get for the Tuesday puzzle: the probability that he has two boys when he mentions a boy born on a Tuesday = the probability that he mentions a boy born on a Tuesday when he has two boys (1/7) times the probability that he has two boys (1/4), divided by the probability that he mentions a boy born on a Tuesday (1/14). Again, we get the result 50%.
In my opinion, this is the correct answer, or a least, the answer that is most probably correct. Returning to the simple boy/girl puzzle, a real everyday situation may contain other factors that change the outcome; for instance, if somebody says “If have two kids, one is a boy” we would normally assume that the other is a girl – else he would probably have said “I have two boys” or “I have two girls”.
As told by Alex Bellos of the New Scientist, Foshee said “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?”. The way I (and just about everybody else, to judge from the response) interpret the situation is this: If he did not have a boy born on a Tuesday, he would have made the pun about some other child, rather than keeping quiet. I am pretty sure that he would have asked “What is the probability I have two girls?” if he had no boys, rather than shut up. Knowing nothing about Foshee’s gender preferences, we must assume that he is equally likely to mention boys or girls, if he has one of each. Thus, we get the answer 50% as stated above.
Alex Bellos elaborates: “The way Foshee meant it is, of all the families with one boy [born on a Tuesday] and exactly one other child, what proportion of those families have two boys?” Quite possibly, but that was not the question he asked. The reason that this seems counter-intuitive is that the whole thing is so contrived, and that the supposedly “correct” answer is the answer to a completely different question than the one stated.
Jesper,
I think you are missing the point here. In your example above, it is true that only 13 people would be left in the room after the “non Tuesday fathers” have left. So 13/27 is a superficially correct answer.
It has no statistical integrity, however, because you still have in the room 12 fathers each of which have a child born on another day.
Now move to the room that the “non-Tuesday fathers” have gone to. Try to repeat the process for Wednesday. You cannot! You would have to excuse yourself and go knock on the Tuesday door and ask if you could please have the two Boy Tuesday Boy Wednesday fathers back because otherwise you can’t make the denominator 27. In other words you can only make the 13/27 work for ALL days of the week (as you must if the Foshee theory is to mean anything) if you also accept that 6/7 of the BB families SHARE fathers between two different days. So these fathers cannot claim with 100 % probability that they are ” a Tuesday father” or a “Wednesday father”.
THAT is why the 13/27 is a fallacy. It is a verbal trick, and to go to the top of the page and your headline, Tuesday changes absolutely nothing.
@sam
“There is NOTHING in Foshee’s statement to say that any such screening has occurred and that Foshee’s family is anything other than a normally (binomially?) distributed family. ”
You are right, nothing in Foshee’s statement suggests that. This is a completely normal family. The 13/27 result is not about boys being particularly likely in this family, but about the fact if you add another parameter (weekday here), the probability of (two boys with at least one born on a Tuesday)/(at least one boy born on a Tuesday) becomes larger than 1/3. 13/27 in this case. The amount of boys does not change, but the question asked in the puzzle is just a different question than what one thinks at first.
@Søren
I am not convinced that you can make calculations on the likelihood that the speaker reveals one gender over another.
The answer to the puzzle: “I have two children, one of them is a girl. What is the chance that I have two girls” – is also 1/3.
You can try flipping coins to see how this works in practice.
Keep flipping two coins simultaneously. Divide the # of throws with two head coins with the # of throws with at least one head coin. You will find that the result approaches 1/3 over time.
@ron
I think you have completely identified the core of the puzzle.
Many sets of children would be counted on both Tuesday and another weekday. This is why the puzzle gives the surprisingly high 13/27 result.
However, the puzzle does not state that no set of children should be counted for more than weekday. It simply asks about the probability of (two boys with at least one born on a Tuesday)/(at least one boy born on a Tuesday). Hence, 13/27.
“I am not convinced that you can make calculations on the likelihood that the speaker reveals one gender over another.” – but I just did… your assertion was disproved before you made it. Although I must admit I made the simplest possible calculation – having no knowledge to speek of about Gary Foshee, I assigned an equal likelihood to all genders (by dividing certainty (1) by the number of known genders) and weekdays (by dividing certainty by the number of known weekdays) and assuming that weekdays and genders were independently distributed. This is a straightforward application of Bayesian probability (and mathematical commen sense): when you have no knowledge, you must assign an equal probability to all possible outcomes.
“You can try flipping coins to see how this works in practice.
Keep flipping two coins simultaneously. Divide the # of throws with two head coins with the # of throws with at least one head coin. You will find that the result approaches 1/3 over time.”
Yes, but what about this game: I keep flipping the two coins, if I get two heads, I ask you “I have two coinss, one of them is a head. What is the chance that I have two heads”, and if I have two tails, I ask “I have two coins, one of them is a tail. What is the chance that I have two tails”, and if I have one of each, I flip another coin to find out which question to ask. You will find that the result approaches 1/2 over time.
What would Foshee have done if he did not have a boy born on a Tuesday? In order to get the solution 13/27, you MUST assume that he would have kept quiet. That is theoretically possible – but then you must answer the question “why Tuesday?” why not some other weekday? And why a boy? why not a girl?
It is theoretically possible that Foshee flipped a coin – “heads, it’s boy, tails means girl”, got heads and counted his children – found out that he had two and at least one of them was a boy – “great, then I may be able to make riddle”, he thought. He then, by a somewhat more cunningly designed procedure, picked a random weekday. “Tuesday, what a wonderful coincidence, I am the father of two children, and at least one of them is a boy born on a Tuesday” – so he proceeded to state his riddle – otherwise he would have practised an Indian Rope Trick for the convention. Theoretically possible, but not very plausible.
Cant agree more with Jan’s post (8th June) on this…. when I read the article in New scientist, obvious answer is 1:2 order has nothing to do with it as it is NOT posed in the original question. Therefore, since he has stated that one of his two children is a boy, then quite obviously (assuming no genetic or environmental factors influence gender predisposition for My foshee and his wife..) then it is 1:2
Quite worrying for the human race that this was reported incorrectly in New Scientist and that so many people cant ‘see’ this…….
Nigel (8th June post)
Your response to Jan is misleading. Reason being that we are not tossing two coins, since we already know one of the coins is say heads (head =boy, tail = girl..or the other way around if you prefer, doesnt matter..) therefore, chance of getitng H/H or H/T is exactly 1:2 as Jan points out…. It makes ALL the difference that Foshee already told us he had a boy…………
MO
cant get any clearer?
Sean Carmody wrote:
To sum up, if Mr Smith volunteers ‘I have two children and at least one is a boy,’ then the probability that he has two boys is 1/2, whereas if you ask him ‘do you have two children and at least one boy’ and he answers ‘yes’, the probability that he has two boys is 1/3. Likewise, if he volunteers that he has a boy born on a Tuesday, the probability that he has two boys is 1/2 but if you ask him whether he does and he says yes, the probability of two boys is 13/27.
taken from this blog.http://www.qi.com/talk/viewtopic.php?t=18947&postdays=0&postorder=asc&start=105
The problem is that Mr Foshee asked the wrong question for the answer he was wanting……..
@søren
As you know, when I said that “I am not convinced that you can make calculations on the likelihood that the speaker reveals one gender over another.”, I meant that this is not a valid calculation. You could also just multiply by 42 or divide by what ever number you choose – but it would not make the result valid either.
But then, we are not really discussing probability at all, but how to interpret the problem statement. The Wikipedia article on the Boy or Girl Paradox has some pointers to the psychology concerning how we interpret such problems.
“What would Foshee have done if he did not have a boy born on a Tuesday? In order to get the solution 13/27, you MUST assume that he would have kept quiet. That is theoretically possible – but then you must answer the question “why Tuesday?” why not some other weekday? And why a boy? why not a girl?”
Well, this is exactly why the result is 13/27. He tells us exactly that he has two children, at least one of them being a boy born on a Tuesday. You calculate all the configurations in which there are two boys, one of which is born on a Tuesday (13), and divide it by the number of configurations in which there is at least one boy born on a Tuesday (27). There is no mention of other weekdays – that is something that you have personally invented, so it can’t really be said to be part of the puzzle.
@MO
“Cant agree more with Jan’s post (8th June) on this…. when I read the article in New scientist, obvious answer is 1:2 order has nothing to do with it as it is NOT posed in the original question. Therefore, since he has stated that one of his two children is a boy, then quite obviously (assuming no genetic or environmental factors influence gender predisposition for Mr Foshee and his wife..) then it is 1:2”
It’s a puzzle because the obvious answer (1/2) is wrong. This is common in discussions of probability. If he had stated that a specific child was a boy, then the answer would be 1/2, but since he states that at least one of them is a boy, then the answer is 1/3.
As I was saying before, the Wikipedia article has more discussion of the psychology around it.
Your response to Jan is misleading. Reason being that we are not tossing two coins, since we already know one of the coins is say heads (head =boy, tail = girl..or the other way around if you prefer, doesn’t matter..) therefore, chance of getting H/H or H/T is exactly 1:2 as Jan points out…. It makes ALL the difference that Foshee already told us he had a boy…………
We know that one of the coins is head. If we knew which one, the result would be 1/2, but since it can be either one, the result is 1/3.
*
OK, I am probably not going to continue this discussion much longer, but I would be happy to play a coin-flipping game with anyone who is up for it:
a) We keep flipping two coins simultaneously.
b) If both coins are tails, we flip the coins again.
c) Otherwise, you give me $15 if there is one head, and I give you $20 if there are two heads.
If the probability is 1/2, you will be making money. If it’s 1/3, I will.
Any takers?
The 13/27 value is erroneous and arises due to inconsistencies in the calculation.
If we ask the question:
“I have two children, one is a boy called Malcolm and he was born on a Tuesday”
This will not change the problem, but does make it a lot easier to explain.
Is Malcolm older or younger than his brother?
Does it matter, or is this question irrelevant?
Either it matters or it doesn’t – you can’t just jump backwards and forwards.
The people who came to the 13/27 value have been inconsistent, sometimes the difference is recognised and other times it is unrecognised.
Error 1
Why does it matter if Malcolm is older or younger than his sister, but not matter when he is older or younger than his brother? – Inconsistent
Error 2
The first section was treated as though it made no difference if Malcolm was older or younger than his brother, but when the days of the week are considered we suddenly find it does matter after all.
– Inconsistent with step 1
Error 3
In the case where both siblings are born on a Tuesday: It is acknowledged that Malcolm being older than his SISTER is different from him being younger. However, it is then assumed that Malcolm being older than his BROTHER is somehow identical to him being younger, leading to the elimination and only 6 outcomes in the final case. What is more, step 2 has just stated that him being younger IS different to him being older so its inconsistent with step 2 as well.
This is just a botched calculation caused by the inconsistent application of assumptions.
Its 50%.
@knoydart
I won’t repeat all of the discussion here, but you can have a look at the the Wikipedia article for an explanation about why the puzzle answer is 1/3 when no weekday is mentioned.
If we ask the question:
“I have two children, one is a boy called Malcolm and he was born on a Tuesday”
This will not change the problem, but does make it a lot easier to explain.
You are, in fact, changing the problem. This is the core of the puzzle.
When talking probability, there is a huge difference between saying “this boy is such and such and I have another child” vs. “I have at least one boy with the following characteristics”. If you don’t believe it, I will happily play the coin-flipping game with you that I discussed in the previous comment.
Jesper,
You did not answer my questions: “What would Foshee have done if he did not have a boy born on a Tuesday?” “Why Tuesday?”
You mentioned the Wikipedia article about the Boy or Girl Paradox – they state the problem as follows: “Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys?”
The article then states “… the critical assumption is how Mr. Smith’s family was selected and how the statement was formed. One possibility is that families with two girls were excluded in which case the answer is 1/3. The other possibility is that the family was selected randomly and then a true statement was made about the family and if there had been two girls in the Smith family, the statement would have been made that “at least one is a girl”. If the Smith family were selected as in the latter case, the answer to question 2 is 1/2.”
Gary Foshee’s family indeed corresponds to the latter possibility, meaning that the probability of the other child being a boy is 1/2. In order to arrive at the probability 1/2, the author of the article has to make the same assumption as I did: that the chances of a boy and a girl being mentioned are equal when there is one of each. If we happen to know, for instance, Gary Foshee is a male chauvinist pig (meaning that he would only mention a girl if he had two girls), but has no preferences for any weekdays, the probability would be 1/3, Tuesday or no Tuesday.
@søren
Well, as the wikipedia article describes, it’s all about how we interpret the statement. I think you interpret it rather strangely, but you are not alone!
You did not answer my questions: “What would Foshee have done if he did not have a boy born on a Tuesday?” “Why Tuesday?”
I didn’t mention it because I am not convinced the question makes any sense. We were given some information (boy, Tuesday, prob of two boys), and we can show that the probabilities would be the same for all other possible combinations (girl, Wednesday, prob of two girls).
Jesper,
Hello again. What do you think to this calculation, done in exactly the same way as the Foshee 13/27 fraction:-
P of two boys if the boy was born between midnight and noon (assuming as always that births occur at regular patterns and birth times of boys and girls are also randomly spread) is 3/7.
It must be true that the probability of two boys if the boy is born between noon and midnight is also 3/7.
So from this we can conclude (I think) that, if a boy is born between midnight and midnight then the probability of a two boy family is 3/7.
So a boy born at any time of the day yields a two-boy probability of 3/7, as opposed to a probability of 1/3 if he is just born.
Withholding the time of his birth apparently reduces the odds from 3/7 back to 1/3
@Ron
I agree with the calculation. As I wrote in the original post, “For a trait with probability 1/A, the probability of having two boys is 2A-1/4A-1.”
In this case, the probability of being born at AM time is 1/2.
So 2*2-1/4*2-1 = 3/7.
Jesper,
That being the case then, we have:
1. For this calculation using the Foshee method of counting the denominator and numerator:-
P of a two child family with a boy born at any time of day = 3/7
2. For the “simple” question, using the Foshee method of counting the denominator and numerator:-
P of a two child family with a boy born at any time of day = 1/3
Does this not question the validity of the Foshee method of calculation when it can produce two contradictory answers?
The comparison to the Monty Hall problem is a good one, because it illustrates how people confuse prior probability with posterior probability (note: I’m not going to be particularly rigorous with terminology here). Prior probability represents the distribution of events before a condition is applied, while posterior probability represents distribution after it is applied (i.e., when events that don’t match the condition are ignored).
A problem statement can be misleading if it is described as an example, because an example only describes posterior events. That is where we need to get the answer from, but their probabilities can never be calculated directly. They must be calculated from the prior probabilities. So we must extrapolate what the condition C was before it was applied, not after. Then, the posterior probability of any event E is the prior probability of E and C happening together, divided by the prior probability of C happening. This is a definition.
The Monty Hall problem is an excellent example. The condition described in the example is that the car is not behind Door #3, which means it is either behind Door #1 or Door #1. The prior probabilities of these two events are 1/3 each. If the naïve solver does not recognize that prior events are different from posterior events, he will say that C is the union of these two *prior* events, with prior probability 2/3. And so the posterior probability the car is behind either door is (1/3)/(2/3)=1/2.
That is wrong, because the condition is not “The car is behind #1 or #2,” it is “The car is behind #1 or #2 AND the host opened #3.” A simple examination of the cases shows that if the car is behind Door #2, the host must always open Door #3; but if the car is behind Door #1, then half the time the host will open Door #2. So half of the Door #1 outcomes in the prior space do not belong in the condition C. Thus:
) The prior probability the car is behind #1 AND host opens #3, is 1/6.
2) The prior probability the car is behind #2 AND host opens #3, is 1/3.
3) The prior probability the host opens #3 is 1/6+1/3=1/2.
4) The posterior probability the car is behind #1 is (1/6)/(1/2)=1/3.
5) The posterior probability the car is behind #2 is (1/3)/(1/2)=2/3.
A very similar analysis can be applied to the Two Child Problem (ignore the Tuesday version for a moment). The condition described in the example seems to say that the family either has one boy (prior probability 1/2) or two boys (prior probability 1/4). Note that I removed order from this, since it is only necessary to establish those probabilities. Again, if the naïve solver does not recognize that prior events are different, he will say the condition C is the union of these two *prior* events, with prior probability 3/4. And so the posterior probability of two boys is (1/4)/(3/4)=1/3.
This is just as wrong as 1/2 was for the Monty Hall Problem, for the exact same reasons. The condition is not “The family is B1 or B2,” is it “The family is B1 or B2 AND the father tells you he has a boy.” IF (let me repeat that: *IF*) you allow that a father of a boy and a girl could tell you “I have two children, and one is a girl,” then half of the B1 cases do not belong in the condition C. Just like half the Door #1 cases didn’t belong in the MHP condition. So:
1) The prior probability of B2 AND the father telling you “I have a boy” is 1/4.
2) The prior probability of B1 AND the father telling you “I have a boy” is 1/4.
3) The prior probability of B1 AND the father telling you “I have a girl” is 1/4.
4) The prior probability of father telling you “I have a boy” is 1/4+1/4=1/2.
4) The posterior probability of two boys is (1/4)/(1/2)=1/2.
When somebody tells you that the answer to the simple version of the Two Child problem is 1/3, that person either is being naïve and not recognizing that prior events are different from posterior events, or believes for some reason that the father was required to tell you about boys if he could. See Keith Devlin’s recent retraction of “1/3” as the answer to Foshee’s simple problem, at http://www.maa.org/devlin/devlin_05_10.html.
Gary Foshee’s answer of 13/27 for the Tuesday Child problem is also the naïve, or “required,” version of the solution. He is treating the posterior event where a father says “I have two children, and one is a boy born on a Tuesday” as equivalent to the prior event of the same description. It seems unintuitive, because we can easily recognize how adding “born on a Tuesday” is applied in the posterior space, not the prior space. That a father of two boys, one born on Tuesday and one born on Friday, could equally well mention the Friday boy.
But since Foshee has been convinced that the naïve solution to the simpler problem is correct, he equally naively applies the same solution to the Tuesday Child version. There is no valid reason to assume the conditions that lead to either are correct. The answer to both of Foshee’s questions is 1/2.
@ron
I am not sure I understand your argument.
The whole point of the Tuesday boy problem is that if you include an extra parameter into the calculation (such as weekday born or time of day), then the probability changes. (Not because it literally “reduces the odds” of having a boy, but because you are calculating something different than the odds of having a boy).
This seems to be exactly what you are saying. Do you think you are saying something different?
@JeffJo
I agree with you (and with Keith Devlin) that the results are largely a question of how you interpret the questions in the first place.
It is also certain that to calculate probability, you have to formulate it as “given A, what is the chance of B”.
I don’t think the “official” results are due to a mixing up for prior and posterior probability – it’s just that you have a different interpretation of the basic problem.
The reason you get the 1/2 result is simply that you are interpreting the question differently: You are calculating the probability for “given that someone with two children has told you the gender of one of this children, what is that chance that the other child is a boy”. This is obviously 1/2.
The “official” interpretation is “given that someone with two children has at least one boy, what is the chance that he has two boys”. This is 1/3.
Jesper,
What I am saying is that, at the end of the day, we have NOT calculated “something different”.
We have calculated EXACTLY the same thing, using the same Foshee methodology, and have come up with two different answers.
@ron
I described the difference in the cocktail party examples above. Are you saying that you don’t think there is a difference between the two cocktail party examples?
Jesper,
What you described in the cocktail party examples were the two different answers you can get to the Tuesday Boy question. I have no problem with your data or conclusions. The reason you get two different answers is that you use two different METHODS of calculating the denominator and numerator. One is the Foshee method resulting in 13/27 and the other is the one I prefer, which gives 1/3.
The question is – “Which method has the greater integrity?”. The “Morning Boy” calculation was done using the Foshee method as was the “simple” question calculation.
They give two DIFFERENT answers to the SAME question (3/7 and 1/3)
Using the second cocktail party method gives a consistent answer of 1/3 for BOTH questions.
Near the top of this thread you said ” The result really is 13/27.”
Jesper – It is not.
@ron
If you believe that these two different methods give different answers for the same question (rather than answering two different questions), then you have uncovered a major flaw in probability theory as it is taught and applied in universities and companies across the world. Just sayin’.
Jesper,
Someone had to do it.
Jesper,
All joking aside, here is ONE question:-
“A two child family has at least one boy. He is born in a period of the calendar called “a day”.
What is the probability that his sibling is a brother?”
Use the Foshee method of counting.
What’s the answer? Is it 1/3, 3/7, 13/27? There are many more answers possible to this ONE question using the Foshee method.